Binary Trees - Learn by visualizing

A Binary Tree is a fundamental concept in computer science used in various algorithms and data structures, such as binary search trees, heaps, and syntax trees.

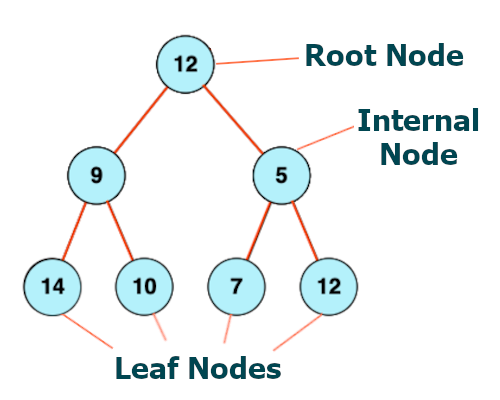
A binary tree is a hierarchical data structure in which each node has at most two children, commonly referred to as the left child and the right child. The topmost node in a binary tree is called the root, while the bottom-most nodes, which have no child nodes, are known as leaf nodes (or simply leaves).

Key Features of a Binary Tree:

Nodes: Each node in a Binary Tree has three parts: Data and references (or pointers) to its left and right children.
Root: The top node in the tree. It is the starting point of the tree structure.
Leaf Nodes: Nodes that do not have any children (i.e., both their left and right pointers are null).
Internal Nodes: Nodes that have at least one child (left or right).
Height: The height of a binary tree is the length of the longest path from the root node to a leaf.

Binary Tree Traversal:

Binary Tree Traversal involves visiting all the nodes of the binary tree in a specific order. Tree traversal algorithms are generally classified into two main categories: Depth-First Search (DFS) and Breadth-First Search (BFS).

In Depth-First Search (DFS), we aim to visit the nodes as deep as possible, starting from the root. DFS has three main traversal techniques:
1. Inorder: Visit the left subtree, then the current node, and then the right subtree.
2. Preorder: Visit the current node, then the left subtree, and finally the right subtree.
3. Postorder: Visit the left subtree, then the right subtree, and finally the current node.
In Breadth-First Search (BFS), we prioritize visiting the node closest to the root before moving on to nodes further away. This approach typically uses a queue to explore each level of the tree from top to bottom.

In the following problems, you will see visualizations demonstrating how these traversal algorithms work in practice.

Applications of Binary Trees:

Searching: Efficient searching (in structures like Binary Search Trees).
Sorting: Binary trees are used in some sorting algorithms (like heaps).
Expression Parsing: Expression trees (used in compilers) represent mathematical expressions.
Hierarchical Data Representation: File systems or organization charts can be represented using binary trees.

Binary trees are fundamental in computer science because of their versatility in various applications like searching, balancing, and tree traversal.

BinaryTrees Problems

Go through some of these binarytree problems and their visualizations!